عدد مرموز پی را بهتر بشناسیم!
تاريخچه:
بابليان هنگامي که ميخواستند مساحت دايره را حساب کنند،مربع شعاع آن را در 3 ضرب ميکردند.البته لوحهاي قديمي تري از بابليان وجود دارد که مشخص ميکند آنها مقدار تقريبي پي را برابر3.125 ميدانستند.در مصر باستان مساحت دايره را با استفاده از فرمولمحاسبه ميکردند.( d قطر دايره در نظر گرفته ميشد )که در نتيجه مقدار تقريبي عدد پي 3.1605 بدست ميآيد.
تقريب اعشاري عدد پي:
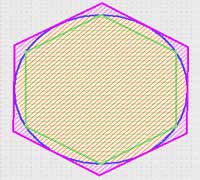
اولين نظريه در مورد مقدار تقريبي عدد پي توسط ارشميدس بيان شد.اين نظريه بر پايه تقريب زدن مساحت دايره بوسيله يک شش ضلعي منتظم
محيطيو يک شش ضلعي منظم محاطي استوار است.
رياضيدانان اروپايي در قرن هفدهم به مقدار واقعي عدد پي نزديکتر شدند.از جمله اين دانشمندان جيمز گريگوري بود که براي پيدا کردن مقدار عدد پي از فرمول زير استفاده کرد:
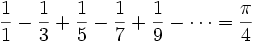
يکي از مشکلاتي که در اين روش وجود دارد اين است که براي پيدا کردن مقدار عدد پي تا 6 رقم اعشار بايد پنج ميليون جمله از سري فوق را با هم جمع کنيم.
در اوايل قرن هجدهم رياضيدان ديگري به نام جان ماشين فرمول گريگوري را اصلاح کرد که اين فرمول امروزه نيز در برنامه هاي رايانه اي براي محاسبه عدد پي مورد استفاده قرار ميگيرد.
اين فرمول به صورت زير است:
 |

با استفاده از اين فرمول يک انگليسي به نام ويليام شانکس مقدار عدد پي را تا 707 رقم اعشار محاسبه کرد،در حاليکه فقط 527رقم آن درست بود.
امروزه مقدار عدد پي با استفاده از پيشرفته ترين رايانه ها تا ميليونها رقم محاسبه شده است. و تعداد اين ارقام هنوز در حال افزايش است.